A) Determine the frequency of the motion
Trying to solve for F (frequency). By using the free body diagram we sum the forces in the x direction (horizontal in the example).
By summing forces in the X axis (positive to the right) we get: Sum of Forces in x = Force of the spring. Steps shown below:
Showing the only force in the X direction is the Force of the spring in the negative direction. | |
A force of a spring is the spring constant times the distance from rest. | |
Substituting the force of the spring in we get (mass)(accell.) = -(spring const.)(distance) |
We are looking to get this into the form to where we can show what the second derivative of x (the position) is equal to a so we can extract omega from it. Acceleration (a) is the second derivative of position (x). Therefore we can solve for (a) from our forces above. Steps:
Solving for a we get: a = -(k/m)x | |
We need to find that second derivative of position equals negative omega times the position (second derivative of x = -(w^2)a). Acceleration is the second derivative of position. We replace a with (d^2/dt^2)x to show that. Notice that k/m is omega squared. | |
Because we got our equation in the correct form, we show that k/m = w^2. Solve for w (omega) we get sqrt(k/m) = w. | |
Plugging in the given values of the problem we can get a numerical answer which is approximately .842169 hertz. |
B) Determine the Period
D) Determine the Maximum Force

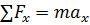
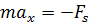














No comments:
Post a Comment