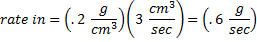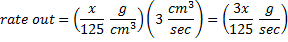We will let x = grams of the drug, t = tine in seconds and the rate is g/sec
Follow the steps below to solve.
| This is a differential equation mixture problem. We can set our initial equation based on (rate in) - (rate out) = dx/dt (or change of x over change in time) | | |
| We know our rate in as (.2 g/cm^3)(3 cm^3/sec). This does give us our correct rate units of g/sec): | | |
| Our rate out is (x/125 g/cm^3)(3 cm^3/sec). x/125 is the amount of drug in the organ at time t. This is always changing and therefore we assign it a variable: | | |
| Now simplified with only our values: | | |
| Collecting like terms to get the dx and the x together and then setting up the integral: | | |
| Integrate both sides. The left side is integrated as follows: | | |
| | | |
| The completed integration equation is shown and the C (constant) has been collected on one side: | | |
| We can use the known initial condition x(0)=0, to solve for C. We know x(0)=0 because at time 0 there was no drug in the organ. | | |
| Rewriting the equation with our constant, C: | | |
| Because of the natural log, ln, we will raise each side to the power of e and we are also multiplying each side by (-3) to be able to solve: | | |
| Simplifying with using the laws of logarithms and exponents: Also note, we can drop the absolute value sign as the constraint of our problem requires it to be positive. | | |
| This only gives us x at time t, or the amount of the drug in grams. The question asks for the concentration of the drug at time t. To find concentration we divide this number by 125 (total capacity) to find the concentration: | | |
| Therefore, our concentration of the drug at time t is: | | |
| Find t when the concentration of the drug reached 0.1 g/cm^3 and simplifying: | | |
| Taking the natural log of both sides and solving for t: | | |
| Final answer for t is approx 28.88 seconds: | | |