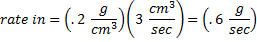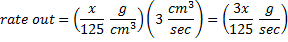Michelson-Morley 2

Verify by calculation that the result of the Michelson-Morley experiment places an upper
limit on Earth’s speed relative to the ether of about 5 km/s.

Because M-M found that N must be less than or equal to 0.01, then his places a maximum velocity limit on this calculation:
Showing the limit mathematically by solving for v with the given information:
The numeric calculation for the above formula is 4.91 km/s

Because the Earth rotates at approximately a rate of 30 km/s, and because the velocity above is much smaller, our calculations imply that the "ether" does not exist. Meaning, there is no preferred reference frame.

Michelson-Morley Experiment 1

A shift of one fringe in the Michelson-Morley experiment would result from a difference
of one wavelength or a change of one period of vibration in the round-trip travel of the light
when the interferometer is rotated by 90°. What speed would Michelson have computed for
Earth’s motion through the ether had the experiment seen a shift of one fringe?

Change in time for the two paths of light:
So we should find fringes for the extra distance that the light travels in time t:
Solving for v:
Given from the M-M Experiment:
Solving for v when N=1, or where the first fringe would have been detected:

Differential Equation, Drug mixture in blood stream

Blood goes into an organ at a rate of 3 cm^3/sec (or cm3/sec) and leaves at the same rate. The organ has a liquid volume of 125 cm^3 (or cm3). A drug is introduced into the blood going into the organ at a concentration of 0.2 g/cm^3. Find a formula for the concentration of the drug at time t (t is time in sec after it is first introduced). When will the concentration of the drug in the organ reach 0.1 g/cm^3?

We will let x = grams of the drug, t = tine in seconds and the rate is g/sec

Follow the steps below to solve.

This is a differential equation mixture problem. We can set our initial equation based on (rate in) - (rate out) = dx/dt (or change of x over change in time)
We know our rate in as (.2 g/cm^3)(3 cm^3/sec). This does give us our correct rate units of g/sec):
Our rate out is (x/125 g/cm^3)(3 cm^3/sec). x/125 is the amount of drug in the organ at time t. This is always changing and therefore we assign it a variable:
Now simplified with only our values:
Collecting like terms to get the dx and the x together and then setting up the integral:
Integrate both sides. The left side is integrated as follows:
The completed integration equation is shown and the C (constant) has been collected on one side:
We can use the known initial condition x(0)=0, to solve for C. We know x(0)=0 because at time 0 there was no drug in the organ.
Rewriting the equation with our constant, C:
Because of the natural log, ln, we will raise each side to the power of e and we are also multiplying each side by (-3) to be able to solve:
Simplifying with using the laws of logarithms and exponents: Also note, we can drop the absolute value sign as the constraint of our problem requires it to be positive.
This only gives us x at time t, or the amount of the drug in grams. The question asks for the concentration of the drug at time t. To find concentration we divide this number by 125 (total capacity) to find the concentration:
Therefore, our concentration of the drug at time t is:
Find t when the concentration of the drug reached 0.1 g/cm^3 and simplifying:
Taking the natural log of both sides and solving for t:
Final answer for t is approx 28.88 seconds: